Forschung > Plan-a-Day > Therapie von Planungsstörungen mit Hilfe von Plan-A-Day - Manual Therapie von Planungsstörungen mit Hilfe von Plan-A-Day - Manual Entwicklung eines Programms zur Diagnostik und Therapie von Planungsstörungen Joachim Funke, Silke Huchler, Susanne Struwe, Jutta Wolf & Thomas Krüger Psychologisches Institut der Universität Bonn und Psychologisches Institut der Universität Heidelberg  Stand: 14.1.97 1 Vorbemerkung 2 Einführung 2.1 Zur Terminologie bei Anforderungen vom Typ PAD 2.2 Exkurs: Zur Bewertung von zeitlichen Überschneidungen 2.3 Mögliche Heuristiken bei der Bearbeitung von PAD 3 Training ausgewählter Heuristiken 3.1 Bisheriger Einsatz des PAD zu Trainingszwecken 3.2 Grundlegendes Trainingsrationale 3.3 Allgemeine Überlegungen zum zeitlichen Ablauf des Trainings 3.3.1 Phase 1: Vorauslaufende Diagnostik 3.3.2 Phase 2: Training 3.3.3 Phase 3: Evaluation des Trainingserfolgs 3.3.4 Weitere Variationen des Phasenablaufs 4 Trainingseinheit "Beachten der Priorität" 4.1 Einschrittige Auftragsmuster 4.2 Mehrschrittige Auftragsmuster 5 Trainingseinheit "Minimierung der Wegzeiten" 5.1 Ziel des Trainings 5.2 Die Struktur der Auftragsblöcke 5.3 Einschrittige Auftragsmuster 5.3.1 Typ W1A: Auftragsblöcke mit zwei Aufträgen ohne Wegzeitangabe 5.3.2 Typ W1B: Auftragsblöcke mit zwei Aufträgen mit Wegzeitangabe 5.3.3 Typ W1C: Auftragsblöcke mit zwei Aufträgen plus Angabe von Zielort 5.3.4 Typ W1D: Auftragsblöcke mit zwei Aufträgen plus Angabe von Zielort plus Autovorteil 5.4 Zweischrittige Auftragsmuster 5.4.1 Typ W2A: Auftragsblöcke mit drei Aufträgen ohne Wegzeitangabe 5.4.2 Typ W2B: Auftragsblöcke mit drei Aufträgen mit Wegzeitangabe 5.4.3 Typ W2C: Auftragsblöcke mit drei Aufträgen plus Autovorteil 6 Trainingseinheit "Maximierung der Auftragserledigung" 6.1 Die Heuristik "Maximierung der Auftragserledigung" 6.2 Faktoren, die die Aufgabenschwierigkeit beeinflußen 6.3 Aufgabenstruktur 6.3.1 Formale Struktur 6.3.2 Schematische Darstellung 6.3.3 Problemanalyse 6.4 Schwierigkeitshierarchie 6.4.1 Auftragsblöcke zu drei Aufträgen 6.4.2 Auftragsblöcke zu vier Aufträgen 6.4.3 Auftragsblöcke zu fünf Aufträgen 7 Ausblick 7.1 Literatur 7.2 Danksagung Zusammenfassung Berichtet wird über Konzeption und Durchführung eines systematischen Programms, mit dem Planungsstörungen gezielt diagnostiziert und trainiert werden können. Dieses Programm bezieht sowohl Übungen am PC als auch herkömmliche Papier-und-Bleistift-Übungen mit ein. Summary: Development of a program for diagnosis and training of planning disturbances (will be translated later) 1 Vorbemerkung Die vorliegende Arbeit entstand im Rahmen einer Kleingruppe, die sich im Kontext einer Lehrveranstaltung im Hauptstudienabschnitt ("Forschungorientierte Vertiefung Kognitionspsychologie") im Sommersemester 1996 am Psychologischen Institut der Universität Bonn konstituiert hat. Ziel dieser forschungsorientierten Lehrveranstaltung war die Einbindung kleiner Gruppen von Studierenden in konkrete Forschungsvorhaben aus dem Gebiet der Neuropsychologie. Der vorliegende Bericht ist das Resultat einer intensiven Auseinandersetzung dieser Arbeitsgruppe mit dem Computerprogramm Plan-a-Day, das zur Diagnostik und Therapie von Planungsstörungen eingesetzt werden kann. In Ergänzung zu dem Computerprogramm sind allerdings auch herkömmliche Papier-und-Bleistift-Übungen vorgesehen, die zu speziellen Zwecken eingesetzt werden können. Wie sehr sich die hier vorgenommene Verbindung von forschungsorientierter Lehre mit den Interessen praktisch arbeitender Neuropsychologen als fruchtbar erweist, werden andere zu beurteilen haben - aus Sicht der Autorinnen und Autoren macht es jedenfalls großen Spaß, an einem Projekt zu arbeiten, dessen praktische Relevanz von Anfang an als nicht gering einzuschätzen ist und dessen methodische Probleme durchaus Spielraum für anspruchsvollere Überlegungen läßt. 2 Einführung Mit dem von Funke und Krüger (1995) entwickelten Computerprogramm Plan-a-Day (PAD) steht ein neues diagnostisches Instrument zur Verfügung, das von der Testperson die Erledigung einer Reihe von Aufgaben unter Beachtung von Randbedingungen verlangt. Von seiner Grundkonzeption her ist der PAD modular angelegt, d.h. es können Aufgaben unterschiedlicher Schwierigkeit ausgewählt werden. Dies erweist sich insbesondere in Verbindung mit gezielten Trainingsprogrammen als nützlich. Bevor wir die von uns vorgeschlagenen Variationen für Trainingszwecke vorstellen und das Rationale unseres Trainingskonzepts vorstellen, wollen wir kurz die Anforderungen beschreiben, die bei Aufgaben vom Typ des PAD an die planende Person gestellt werden. Bei dieser Gelegenheit wollen wir auch einige Grundbegriffe erläutern, die zum Verständnis späterer Variationen hilfreich sind. 2.1 Zur Terminologie bei Anforderungen vom Typ PAD Um die Anforderungen vom Typ PAD besser verstehen zu können, wird nachfolgend ganz kurz eine typische Aufgabenstellung aus der Standardversion des PAD beschrieben. Hier zunächst die (geringfügig modifizierte) Instruktion. Ihre Aufgabe ist es, Ihren Terminplan für zwei fiktive Tage zu erstellen. Sie sollen auf einem weitläufigen Betriebsgelände möglichst viele Aufgaben erfüllen. Diese dauern jeweils eine gewisse Zeit und sind manchmal auch nur zu bestimmten Zeiten möglich. Auch haben Sie unterschiedliche Wichtigkeit. Zu beachten haben Sie schließlich noch die benötigten Wegzeiten zwischen den einzelnen Orten auf dem Gelände, die jeweils eingeblendet werden. Sie haben für die Erstellung eines Tagesplans maximal 20 Minuten Zeit. Auf dem Monitor wird Ihnen ein Lageplan des Betriebes dargeboten. Bei den Gebäuden erscheint die von Ihrem jeweiligen Ort aus benötigte Wegzeit. Durch Eingabe des jeweils ERSTEN BUCHSTABENS können Sie zu jedem Ort gelangen. Jeweils eine Strecke können Sie mit dem Auto fahren. Am Ziel werden Sie dann gefragt, ob Sie die unter Umständen anfallende Aufgabe zu diesem Zeitpunkt erledigen wollen. Ihr Tagesplan beginnt um 10:00 im Büro. Hier ist die Liste der Aufträge: 1. Zwischen 12:00 und 13:00 können Sie sich in der Cafeteria treffen. Das Gespräch wird dann 45 Minuten dauern. SEHR WICHTIG. 2. Zwischen 10:00 und 13:30 sollen Sie bei der Postzentrale sein. Dies wird dann 45 Minuten dauern. SEHR WICHTIG. 3. Bis 11:30 Uhr müssen Sie bei der Sekretärin sein und dann einen Brief diktieren. Dies wird dann 15 Minuten dauern. 4. Zwischen 10:00 und 13:30 sollen Sie in die Druckerei kommen und dann ein Buch kopieren. Dies dauert 60 Minuten. WICHTIG. Mit dieser Instruktion werden die Aufgabenstellung wie auch die zur Bearbeitung angebotenen Hilfsmittel deutlich, mit denen sich eine Testperson im PAD konfrontiert sieht. Natürlich gehört auch das in Abb. 2.1 gezeigte Display hierzu. 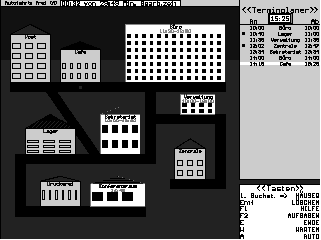Abb. 2.1: Die Oberfläche der PAD-Standardversion, wie sie dem Probanden erscheint. Links der Lageplan mit den Wegzeiten, rechts die Liste der erledigten Aufgaben sowie die Liste mit weiteren Informationsmöglichkeiten. Zu den terminologischen Vereinbarungen, die wir für den nachfolgenden Text festlegen wollen, gehören eine Reihe von Begriffen, die die eben dargestellte Aufgabenstellung formal charakterisieren. Da wir ganze Serien von Aufgabenstellungen entworfen haben, ist es wichtig, die verschiedenen Variationsmöglichkeiten zu kennen. Auch hierfür haben wir Konventionen eingeführt, die wir ebenfalls kurz vorstellen möchten. Als erstes sprechen wir von der Menge aller Aufträge als einem Auftragsblock. Im Beispiel der Instruktionen besteht der Aufgabenblock aus genau vier Aufträgen. Sowohl für einen jeweiligen Auftragsblock als auch für jeweils einzelne Aufträge kann man charakteristische Merkmale nennen. Auf beide Bereiche wird nachfolgend eingegangen. Eigenschaften eines einzelnen Auftrags. Ein Auftrag hat eine frühestmögliche Anfangszeit (FAZ; Zeitpunkt, zu dem frühestens mit der Auftragsbearbeitung begonnen werden kann), eine spätestmögliche Erledigungszeit (SEZ; Zeitpunkt, zu dem spätestens der Auftrag erledigt sein muß), eine Auftragsdauer (A; Dauer der Auftragsbearbeitung) und gegebenenfalls eine Pufferzeit (PZ; wenn die Differenz zwischen SEZ und FAZ größer als AD ausfällt, entsteht PZ, formal: PZ:=[SEZ-FAZ]-AD). Beim ersten Auftrag aus dem obigen Beispiel etwa beträgt die FAZ 12:00 Uhr, SEZ 13:00, AD 45 min und FZ 15 min. FAZ plus PZ ergibt den Zeitpunkt, zu dem man spätestens mit der Auftragsbearbeitung beginnen muß, wenn man mit Erreichen von SEZ fertig sein möchte. Aus dieser Formalisierung ergeben sich zwei Klassen von Aufträgen: Aufträge mit fixem Termin und Aufträge mit variablem Termin. Sie unterscheiden sich danach, ob Pufferzeit vorhanden ist oder nicht; ist PZ=0, handelt es sich um einen Fixtermin, der hinsichtlich der Planungsanforderung stärkere Restriktionen stellt als ein Auftrag mit variablem Termin, der sich durch eine entsprechend große Pufferzeit auszeichnet, in der die Auftragserledigung beginnen kann. Je größer PZ, umso mehr Freiheitsgrade hat die planende Person. Im Beispielblock aus der Instruktion gibt es nur Aufträge mit variablem Termin. Zusätzlich zu diesen Angaben kommen noch Informationen hinzu über den Ort des Geschehens, die eventuell gegebene Prioritätsstufe des Auftrags sowie eine gegebenenfalls vorliegende logische Abhängigkeit des aktuellen Auftrags von einem anderen Auftrag im Auftragsblock (z.B. wenn das häusliche Einräumen gekaufter Tiefkühlkost von ihrem vorherigen Einkauf abhängig gemacht wird). Im Umfeld einer konkreten Auftragserledigung kann es auch eine zugehörige Wegzeit sowie eine eventuelle Wartezeit geben; erstere gibt an, wieviel Zeit auf dem Weg zum aktuellen Auftrag vergangen ist, letztere zeigt an, ob die planende Person vor dem mit FAZ festgelegten Termin am Erledigungsort eingetroffen ist und auf die FAZ wartet. Eigenschaften eines Auftragsblocks. Planungsprobleme inerhalb des PAD entstehen immer erst durch das Zusammenführen mehrerer Aufträge in einem Auftragsblock. Für diesen gibt es ebenfalls einige charakteristische Merkmale. Neben der Anzahl der Aufträge und der Anzahl abhängiger Aufträge beschreibt die Anzahl nicht erledigbarer Aufträge die Menge an Aufträgen, die man unerledigt zurücklassen muß, wenn man die optimale Lösung findet (natürlich ist dies in den leichteren Auftragsblöcken die Menge Null). Ausgezählt wird ferner die Anzahl der Aufträge mit fixem und der mit variablem Zeitpunkt. Die Angabe von Wegzeiten kann in einigen Blöcken ebenso entfallen wie die Angabe von Prioritäten - beides sind daher dichotome Merkmale. Auch das Vorliegen des Autovorteils wird als solches gewertet, obwohl man darüber nachdenken kann, diesen Joker auch zwei- oder mehrfach zur Verfügung zu stellen - allerdings verlöre er damit seinen besonderen Status. Schließlich ist die Anzahl an Überschneidungen zwischen Aufträgen eine wichtige Eigenschaft eines Auftragsblocks. Da dies ein nicht ganz einfaches Thema ist, soll in einem kurzen Exkurs diese Problematik dargestellt werden. 2.2 Exkurs: Zur Bewertung von zeitlichen Überschneidungen Ein nicht unwichtiges Kriterium für die Komplexität von Planungsanforderungen ist die Menge an Überschneidungen zwischen zwei oder mehreren Plänen. Während klar ist, daß ein überschneidungsfreier Satz an Aufträgen sicher in die leichteste Anforderungskategorie zu fallen hat, ist es wesentlich schwieriger, das Ausmaß an Überschneidungen zu quantifizieren. Wir wollen dieses Problem an einigen Beispielen illustrieren und mögliche Lösungsvorschläge zur Quantifizierung der Anforderungskomplexität diskutieren. Abb. 2.2 zeigt zunächst einige Grundformen an Überschneidungen, die für die folgenden Diskussionen zugrundegelegt werden. Wir nehmen dabei vereinfachend an, daß keine zusätzlichen Wegzeiten zu berücksichtigen sind. 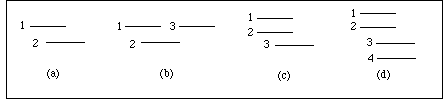Abb. 2.2: Darstellung verschiedener Varianten von Überschneidungen: (a) einfache Überschneidung, (b) Überschneidung, (c) und (d) multiple Überschneidungen. Während die in Abb. 2.2 unter (a) gezeigte Situation zweier sich überschneidender Aufträge 1 und 2 den einfachsten Fall genau einer Überschneidung darstellt (und somit nur jeweils genau 1 Auftrag zu erledigen ist, nämlich entweder 1 oder 2), wird Fall (b) schon interessanter. Da sich Auftrag 2 sowohl mit 1 als auch mit 3 überschneidet, könnte man hier bereits vom Vorliegen zweier Überschneidungen sprechen. Faktisch ist jedoch genau wie vorher nur ein Auftrag, der Auftrag 2, störend. Überschneidungen bestehen zwischen 1 und 2 sowie zwischen 2 und 3, nicht aber zwischen 1 und 3. Die Problemlösung kann somit darin bestehen, entweder Aufträge 1 und 3 oder Auftrag 2 zu erledigen. In Fall (c) sind erneut nur 3 Aufträge beteiligt, diesmal bestehen drei Alternativen zur Problemlösung, nämlich jeweils genau einen der drei Aufträge zu erledigen. Überschneidungen bestehen zwischen 1 und 2, 1 und 3 sowie zwischen 2 und 3. Damit wird deutlich, daß das Konzept der Überschneidung auf der Beurteilung von jeweils genau zwei Aufträgen besteht. Bei mehreren Aufträgen müssen alle möglichen paarweisen Kombinationen betrachtet werden. Generell bestehen bei n Aufträgen n über 2 paarweise mögliche Überschneidungen, bei 3 Aufträgen also 3*(3-1)/2=3 mögliche Überschneidungen, bei 4 Aufträgen 4*(4-1)/2=6 mögliche Überschneidungen. Mit zunehmender Auftragsmenge steigt somit die Zahl möglicher Überschneidungen erheblich an. Ein möglicher Indikator für die Schwierigkeit der Planungskonstellation kann also neben der reinen Anzahl tatsächlicher Überschneidungen sein, wie groß die Anzahl der tatsächlichen Überschneidungen im Verhältnis zu den insgesamt möglichen Überschneidungen ausfällt. Dieser relative Index würde es möglich machen, auch unterschiedlich große Auftragsblöcke in dieser Hinsicht vergleichen zu können. Ein weiterer Problembereich bei diesem Thema betrifft die Frage, ob Überschneidungen zwischen Aufträgen ermittelt werden können, ohne dabei Wegzeiten einzubeziehen. Dieses Problem rührt daher, daß die vorstehend gemachten Ausführungen keine Wegzeiten berücksichtigt haben, also von der Annahme ausgehen, alle Aufträge könnten am selben Ort erledigt werden. In Plan-a-Day ist genau die gegenteilige Situation realisiert. Es gibt nicht zwei Aufträge am selben Ort, was bedeutet: Für jeden Auftrag ist zusätzlich zur Erledigungszeit noch eine Wegzeit einzuplanen. In diesem Fall kann es vorkommen, daß zeitlich überschnittsfreie Auftragsmengen dennoch nicht problemlos bewältigt werden können, da durch Hinzuziehung der Wegzeiten plötzlich Kollisionen entstehen. Abb. 2.3a verdeutlicht diese Situation. 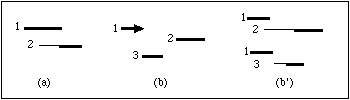Abb. 2.3: Darstellung verschiedener Varianten von Überschneidungen unter Einbezug von Wegzeiten (dünner Strich): (a) einfache Überschneidung, (b) ein Auftragsmuster ohne und (b') mit jeweiligen Wegzeiten. Diese Wegzeiten stellen insofern ein Problem dar, als je nach aktuellem Ort, an dem sich der Planende befindet, unterschiedliche Wegzeiten zu berücksichtigen sind. In allgemeiner Form könnten Wegzeiten daher nur so einbezogen werden, als man für die jeweils paarweise entstehenden Wegzeiten eine Prüfung vornimmt. Abb. 2.3b verdeutlicht dies an einer Situation mit drei Aufträgen, die ohne Beachtung der Wegzeiten überschnittsfrei in der Reihenfolge 1-2-3 bewältigt werden könnten. Beachtet man jedoch die Wegzeiten von 1 nach 2 bzw. von 1 nach 3, wie in Abb. 2.3b` gezeigt, fällt die Reihenfolge 1-2 wegen zu langem Weg aus und nur Abfolge 1-3 ist machbar. Zusammenfassend: Überschneidungen werden immer durch den paarweisen Vergleich von Aufträgen ermittelt. Dabei ist jeweils der Einbezug der paarweise vorliegenden Wegzeiten notwendig. Neben der absoluten Anzahl von Überschneidungn kann auch der relative Anteil bestimmt werden, um Auftragsblöcke mit unterschiedlicher Auftragszahl vergleichbar zu machen. 2.3 Mögliche Heuristiken bei der Bearbeitung von PAD Aufgaben vom Typ des PAD werden von menschlichen Individuen nicht nach Methoden der "Operations Research" bearbeitet, sondern unter Verwendung sog. Heuristiken. Heuristiken sind Regeln, die bei Entscheidungen unter Unsicherheit als Entscheidungshilfen herangezogen werden. Als mögliche Heuristiken bei der Bearbeitung von PAD-Aufgaben haben FUNKE und KRÜGER (1995, p. 110) genannt: (1) Versuche als Nächstes, die in der Nähe liegenden Aufträge zu erledigen ("Minimierung der Wegzeiten"). (2) Versuche den Joker "Autofahrt" auf einer langen Strecke zu verwenden, um die dadurch erreichbare Zeitersparnis zu maximierten ("Maximierung des Autovorteils"). (3) Hoch prioritäre Aufgaben sind mehr zu berücksichtigen als niedrig prioritäre ("Priorität beachten"). (4) Versuche zunächst die Aufgaben zu erledigen, deren spätester Erledigungszeitpunkt am frühesten liegt ("Dringlichkeit"). (5) Vermeide zuviel Wartezeit ("Maximierung der Effizienz"). (6) Arrangiere den Plan um die Fixtermine ("zuerst Fixtermine"). (7) Besuche nur Orte, an denen noch Aufgaben erledigt werden können ("Vermeidung von unsinnigen Besuchen"). (8) Versuche soviel Aufträge wie möglich zu erledigen ("Maximierung der Auftragserledigung"). Unter dem Aspekt des Trainings spezieller Heuristiken könnte z.B. die Aufgabenbearbeitung ausschließlich unter dem Aspekt erfolgen, daß eine ganz spezielle Heuristik optimiert wird. Die Aufgaben sollten so gestaltet sein, daß unter mehreren Alternativen genau eine existiert, die im Sinne der zu trainierenden Heuristik (und möglichst nur in deren Sinne) optimal ist. So wäre es z.B. denkbar, zum Training der Heuristik "Prioritäten beachten" einen Aufgabenblock so zu konstruieren, daß zu einem bestimmten Zeitpunkt immer mehrere Parallelaufträge existieren, von denen aber jeweils nur genau einer die höchste Prirität hat und demzufolge auszuwählen ist. Eine entsprechende Detailanalyse der Aufgabenbearbeitung könnte quantifizierbaren Aufschluß über die Effizienz der Vp in Hinblick auf diese Heuristiken geben und zugleich Hinweise auf durchzuführende Trainings liefern, die die Schwächen der jeweiligen Vp auszugleichen versuchen. Aufgabe des Projekts ist es also, solche Aufgaben zu konstruieren, die besonders "lupenrein" die entsprechende Anforderung abbilden und meßbar machen. 3 Training ausgewählter Heuristiken Im nachfolgend beschriebenen Trainingsprogramm haben wir uns zunächst einmal auf drei dieser Heuristiken konzentriert, nämlich Minimierung der Wegzeiten, Beachten der Priorität und Maximierung der Auftragserledigung. Bevor wir dies im Detail darstellen, soll kurz auf bisherige Trainingsstudien mit dem PAD in seiner Standardversion hingewiesen werden. Danach erläutern wir das grundlegende Rationale für ein Trainingsprogramm spezifischer Heuristiken und stellen allgemeine Überlegungen zum zeitlichen Ablauf eines derartigen Trainings vor. Danach werden die Trainings zu den drei ausgewählten Heuristiken im Detail vorgestellt. 3.1 Bisheriger Einsatz des PAD zu Trainingszwecken KOHLER, POSER und SCHÖNLE (1995) berichten über den erfolgreichen Einsatz des PAD im Rahmen der neuropsychologischen Diagnostik und Therapie. Allerdings sind dafür bestimmte Veränderungen vorzunehmen, die der spezifischen Leistungsfähigkeit neuropsychologischer Patienten Rechnung tragen. Neben einer geringfügigen Veränderung der Oberfläche (vor allem in Hinblick auf gedächtnisentlastende Darstellung) sind es vor allem die Aufgabenstellungen, die auf die spezifischen Bedürfnisse neu zugeschnitten werden müssen. Nachfolgend werden wir beschreiben, wie ein systematisches Training unter Einbezug spezieller Heuristiken gestaltet werden könnte. Allerdings sind für die Anwendung im Rahmen neuropsychologischer Diagnostik und Therapie bestimmte Veränderungen sowohl an der Programmoberfläche als auch an den einzusetzenden Auftragsblöcken vorzunehmen, die der spezifischen Leistungsfähigkeit entsprechend geschädigter Patienten Rechnung tragen. Neben einer geringfügigen Veränderung der Oberfläche (vor allem in Hinblick auf gedächtnisentlastende Darstellung) sind es vor allem die Aufgabenstellungen, die auf die spezifischen Bedürfnisse neu zugeschnitten werden müssen. Nachfolgend werden wir beschreiben, wie ein systematisches Training unter Einbezug spezieller Heuristiken gestaltet werden könnte. 3.2 Grundlegendes Trainingsrationale Um das Augenmerk einer Testperson auf die von uns jeweils in den Mittelpunkt gestellte Heuristik zu lenken, ist folgende Anforderung zu gewährleisten. Die Testperson muß in eine Entscheidungssituation gebracht werden, die ohne Verwendung der Heuristik ein Problem darstellt, mit Verwendung der Heuristik dagegen eine bloße Aufgabe darstellt. Die Unterscheidung zwischen Problem und Aufgabe bezieht sich in Anlehnung an die in der denkpsychologischen Literatur gebräuchlichen Differenzierung darauf, ob für die Lösung eines anstehenden Problems bereits Mittel verfügbar sind (= Aufgabe) oder ob man erst einmal Methoden zur Problemlösung konstruieren muß (= Problem). In bezug auf unsere PAD-Situation heißt dies konkret: Testpersonen werden vor eines der in Abb. 4 gezeigten drei Entscheidungsprobleme gestellt, bei denen alle sonstigen entscheidungsrelevanten Parameter der verschiedenen Aufträge konstant bzw. vergleichbar gehalten werden bis auf genau einen Unterschied, der für die Anwendung der Heuristik allerdings maßgeblich ist. Abb. 3.1: Die drei Grundprobleme in bezug auf die jeweils zu trainierenden Heuristiken (a) Minimierung der Wegzeiten, (b) Beachten der Priorität und (c) Maximierung der Auftragserledigung. In Abb. 3.1a geht es um die Minimierung der Wegzeiten: Von A aus können im nächsten Schritt sowohl B oder C erledigt werden. Eine Entscheidung wird hier möglich, indem man die kürzere Wegstrecke zum Auswahlkriterium macht. Selbstverständlich verkompliziert sich die Grundform dieser Entscheidung mit wachsender Zahl an Aufträgen, aber die alleinige Entscheidungsrelevanz der Wegzeiten sollte in den realisierten Aufgabenblöcken immer gegeben sein. In Abb. 3.1b geht es um das Beachten der Priorität: Zu ein- und demselben Zeitpunkt (und am selben Ort) muß eine Entscheidung zwischen Auftrag 1 oder Auftrag 2 getroffen werden - natürlich unterscheidet sich hier die Priorität derart, daß z.B. Auftag 1 höchste Priorität besitzt und Auftrag 2 nicht wichtig ist. In Abb. 3.1c geht es um die Maximierung der Auftragserledigung. Die planende Person kann entweder den Auftrag 1 oder die zeitgleich zu 1 liegenden Aufträge 2,3 und 4 erledigen. Die Entscheidung für die letztgenannte Option ist im Lichte der genannten Heuristik zwingend. Alle drei Situationen stellen die planende Person somit vor Entscheidungsdilemma, das sich bei Einsatz der entsprechenden Heuristik in Wohlgefallen auflöst. Wichtig für die Konstruktion der Aufgaben ist hierbei, daß nicht andere Kriterien das Dilemma entscheiden helfen. Dies bedeutet: Wenn es um die Minimierung der Wegzeiten geht, darf etwa die Frage der Priorität oder die der Auftragsmaximierung keine Rolle spielen. Hinsichtlich der als jeweils irrelevant betrachteten Merkmale sollte also eine maximale Relaxierung der Restritkionen erfolgen. Wie dies im einzelnen realisiert wurde, wird weiter unten für die drei Trainingseinheiten detaillierter beschrieben. Zunächst sollen ein paar allgemeine Überlegungen zum zeitlichen Ablauf des Trainings gemacht werden. 3.3 Allgemeine Überlegungen zum zeitlichen Ablauf des Trainings Nach unseren Vorstellungen sollte ein Trainingsprogramm mehrphasig angelegt sein. Die drei nachfolgend geschilderten Phasen der vorauslaufenden Diagnostik, des eigentlichen Trainings und der daran anschließenden Evaluation des Trainingserfolgs stellen unserer Ansicht nach das Minimum dar. Phase 1: Vorauslaufende Diagnostik In dieser ersten Phase geht es darum, die Ausgangssituation möglichst differenziert zu erfassen. Zu diesem Zweck sollte aus jeder der Trainingseinheiten mindestens ein Baustein zu diagnostischen Zwecken eingesetzt werden. Das Resultat dieser Phase ist ein individuelles Stärken- und Schwächenprofil, das die Leistungen der Testperson in Hinblick auf die von uns unterschiedenen Heuristiken beschreibt. Phase 2: Training In dieser Phase findet die eigentliche Intervention statt. Entsprechend den Ergebnissen aus Phase 1 wird ein differentielles Training durchgeführt, in dem insbesondere die Bereiche mit Schwächen einem intensiven und spezifischen Training unterzogen werden. Phase 3: Evaluation des Trainingserfolgs Die letzte Phase dient dazu, den Erfolg von Phase 2 zu überprüfen. Mit Testeinheiten, die denjenigen aus Phase 1 vergleichbar sein können, wird erneut ein individuelles Stärken- und Schwächenprofil ermittelt. Wenn das Training in Phase 2 erfolgreich gewesen ist, sollten die in Phase 1 als schwach eruierten Leistungen nunmehr besser bewältigt werden können. Weitere Variationen des Phasenablaufs Selbstverständlich stellt das dargestellte dreiphasige Programm nur das Grundmuster unserer Konzeption dar. Variationen könnten z.B. darin bestehen, im Anschluß an Phase 3 die dort möglicherweise festgestellten, immer noch vorhandenen Schwächen einem erneuten Training zu unterziehen, also Phase 3 im wesentlichen als Eingangsphase 1 zu betrachten und erneut mit Phasen 2 und 3 fortzufahren. Derartige Vorgehensweisen sollten von den Ergebnissen des Einzelfalls abhängig gemacht werden. Auf keinen Fall schiene uns eine sklavische Abarbeitung des geschilderten dreiphasigen Ablaufs wünschenswert. 4 Trainingseinheit "Maximierung der Auftragserledigung" 4.1 Ziel des Trainings Ziel bei der Bearbeitung von Auftragsblöcken unter der Heuristik "Maximierung der Auftragserledigung" ist es, in einem vorgegebenen Zeitraum (10:00 bis 18:00) so viele Aufträge wie möglich zu bearbeiten. Bei diesem Aufgabentyp spielt die zeitliche Dimension eine zentrale Rolle, die Wegzeiten sind deshalb immer angegeben. Somit ist für die Heuristik die Reihenfolge, in der die Aufträge erledigt werden von vorrangiger Bedeutung. Dabei muß beachtet werden, daß es verschiedene Arten von Aufträgen, fixe und variable, gibt. Variable Aufträge müssen, damit sie ebenfalls bearbeitet werden können, in ihrer zeitlichen Abfolge um fixe Aufträge herum plaziert werden. Da sich die einzelnen Zeiträume, in denen Aufträge erledigt werden können, oft überschneiden, wird diese Aufgabenstellung mit zunehmender Auftragsanzahl unübersichtlicher. Je weniger ein fester zeitlicher Rahmen vorgegeben ist, d.h. je mehr variable Aufträge vorliegen, desto komplizierter wird es, einen Bearbeitungsplan zu entwickeln, und desto mehr vorausschauendes Denken ist vermutlich notwendig. Im folgenden werden Schwierigkeitsfaktoren, die bei der Bearbeitung der Auftragsblöcke entsprechend dieser Heuristik eine wichtige Rolle spielen, näher erläutert. 4.2 Einflußfaktoren auf die Aufgabenschwierigkeit Die Schwierigkeit eines Aufgabenblockes kann unter der Heuristik "Maximierung der Auftragserledigung" v.a. durch folgende Faktoren beeinflußt werden: n Anzahl der Aufträge: Je größer die Anzahl der Aufträge, desto schwerer bzw. komplizierter müßte die Planung einer sinnvollen Bearbeitungsreihenfolge werden. Die Anzahl der Aufträge wird im vorliegenden Trainingsset von drei bis maximal fünf variiert. n Zeitliche Stabilität: Es werden fixe und variable Aufträge unterschieden. Liegen nur fixe Aufträge vor, bleibt dem Aufgabenbearbeiter kein Spielraum bezüglich der Reihenfolge der Bearbeitung der einzelnen Aufträge. Sobald jedoch variable Aufträge ergänzt werden, können die Aufträge flexibler erledigt werden. Damit könnte auch die Schwierigkeit steigen, die optimale Bearbeitungsreihenfolge zu finden, d.h. die Reihenfolge bei der maximal viele Aufträge erledigt werden können. n Zwang zur Unvollständigkeit: Ein einfacher Zwang zur Unvollständigkeit liegt vor, wenn ein Auftrag nicht bearbeitet werden kann, weil er zeitlich parallel zu anderen Aufträgen liegt. Unter der Zielsetzung "Maximierung der Auftragserledigung" liegt der unlösbare Auftrag so, daß die Anzahl der Aufträge, die im zeitlich vorgegebenen Rahmen erledigt werden können, bei Bearbeitung dieses Auftrages abnimmt. Es ist also eine optimale Lösung für die Wahl der zu bearbeitenden Aufträge vorgegeben. Der Zwang zur Unvollständigkeit kann auch mehrfach vorliegen, d.h. maximal vierfach bei fünf Aufträgen, von denen vier zeitlich unlösbar sind. Die Aufgabenschwierigkeit müßte sich mit der Anzahl des Zwangs zur Unvollständigkeit verändern. n Anzahl der Überschneidungen: Sie variiert im vorliegenden Trainingsset von null bis maximal zehn, bei fünf Aufträgen. Sind alle Aufträge zeitlich so verteilt, daß keine Überschneidungen vorliegen, ist eine richtige Bearbeitungsreihenfolge bereits vorgegben. Es können aber auch alle Aufträge parallel liegen, d.h. sie überschneiden sich alle zeitlich. Auch dieser Fall ist einfach, weil unabhängig von Art und Anzahl an Aufträgen immer nur einer realisiert werden kann. Eine für die Heuristik "Maximierung der Auftragserledigung" sinnvolle Anzahl an Überschneidungen befindet sich zwischen diesen beiden Extremfällen. Die Schwierigkeit ist vermutlich dann am höchsten, wenn ein hohes Maß an Überschneidungen gegeben ist, die Aufträge sich gegenseitig aber nur zum Teil ausschließen. n Zeitliche Reihenfolge der Zeiträume, in denen variable Aufträge erledigt werden können: Liegen zwei variable Aufträge B und C vor, so ist für jeden Auftrag ein entsprechender Zeitraum B` bzw. C` angegeben, in dem mit der Erledigung des Auftrags begonnen werden kann. Durch die Reihenfolge in der die Zeiträume B` und C` beginnen wird implizit eine ideale Bearbeitungsreihenfolge der Aufträge angeboten, nämlich zuerst B und dann C. Diese implizit vorgegebene Reihenfolge wird z.T. bewußt umgekehrt, wodurch die Schwierigkeit der Aufgabenbearbeitung ansteigen sollte. n Abhängige Aufträge: Ein Auftrag E ist abhängig von einem Auftrag D, wenn die Erledigung des Auftrages D eine notwendige Voraussetzung für die Bearbeitung des Auftrages E darstellt. Die Einführung von abhängigen Aufträgen sollte zu einer Erhöhung der Aufgabenschwierigkeit führen. Die Komplexität des Auftragsblockes steigt, da ein neuer Faktor bei Planung der Auftragserledigung berücksichtigt werden muß. 4.3 Struktur der Auftragsblöcke Im Manual wird für die Heuristik "Maximierung der Auftragserledigung" die Struktur aller Auftragsblöcke detailliert dargestellt. Es folgen dort immer zwei der Schwierigkeit nach parallelisierte Auftragsblöcke aufeinander. An dieser Stelle wird das zugrunde liegende Konzept exemplarisch für den Auftragsblock 101 erläutert. Für jeden Auftragsblock sind der Aufgabentyp und die dazugehörige Configurationsdatei angegeben: Problem 101: Typ A3A; 101.CFG (CFG = Configurationsdatei) 4.3.1 Display auf dem Bildschirm: Unter diesem Punkt finden Sie jeweils die Anweisung, die der Patient zum entsprechenden Auftragsblock auf dem Bildschirm sehen kann. Display auf dem Bildschirm für den Auftragsblock 101: Sie starten von zu Hause. 1. Sie haben um 13:00 einen Arzttermin. Dieser dauert 60 Min. 2. Bei der Versicherung haben Sie um 11:00 ein 30-minütiges Beratungs- gespräch. 3. Im Kulturzentrum können Sie von 10:00 bis 14:15 Bücher ausleihen. Es dauert 45 Min. 4.3.2 Formale Struktur: Anschließend wird die den Auftragsblöcken zugrunde liegende formale Struktur tabellarisch dargestellt. Jedem Auftragsblock ist eine nach ihm numerierte Tabelle zugeordnet. Diese gliedert sich in zwei Abschnitte. Der erste Teil der Tabelle ( die Spalten eins und zwei, von links nach rechts gelesen) bezieht sich auf Merkmale, die für den gesamten Aufgabenblock spezifisch sind. Im zweiten Teil der Tabelle ( Spalten drei bis acht) werden die einzelnen Aufträge näher charakterisiert. Unter dem Punkt "optimaler Rangplatz" ist ihre ideale Bearbeitungsreihenfolge angegeben. Formale Struktur des Auftragblocks 101: Blocknummer 101 Aufträge einzeln A Nr. 1 2 3 Anzahl A 3 A abhängig von A Nr. 0 0 0 Anzahl A abhängig 0 A Dauer (min) 60 30 45 Anzahl A fix 3 Anzahl A variabel 0 frühestmöglicher Anfang 13:30 11:00 10:00 spätestmögliches Ende 14:30 11:30 15:00 Anzahl nicht erledigbarer A 0 Pufferzeit (min.) 0 0 270 Anzahl Autovorteil 0 Anzahl Überschneidungen 2 frühestmöglicher Anfang spätestmögliches Ende Wegzeiten (J/N) J Pufferzeit (min.) Prioritäten (J/N) N Startort Z Priorität Erledigungsort A V K optimaler Rangplatz 3 1 2 Tab. 1: Formale Struktur des Auftragsblocks 101 4.3.3 Schematische Darstellung In einer schematischen Darstellung werden für jeden Auftragsblock folgende Daten veranschaulicht: * die Wegzeiten der einzelnen Aufträge, * die Auftragsdauer, * die Erledigungszeiträume von zeitlich variablen Aufträgen, * die Anzahl zeitlicher Überschneidungen einzelner Aufträge und * die Anzahl unlösbarer Aufträge (auch als Zwang zur Unvollständigkeit bezeichnet). Die genauen zeitlichen Daten finden dabei jedoch keine Berücksichtigung. 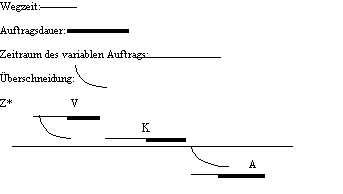Schematische Darstellung für den Auftragsblock 101: Abb. : Schematische Darstellung des Auftragsblocks 101: Mit * wird dabei jeweils der Startort innerhalb eines Auftragsblockes bzw. eines Tagesplanes gekennzeichnet. Bei Auftragsblock 101 ist das Z*, was dem Ausgangsort "Zu Hause" entspricht. 4.3.4 Problemanalyse Für jeden Auftragsblock erfolgt eine Problemanalyse, die abgesehen von der Benennung der einzelnen Aufträge mit unterschiedlichen Erledigungsorten und der zeitlichen Anordnung der einzelnen Aufträge, für jede Parallelversion identisch ist. In der Problemanalyse wird die Problemstellung bzw. die Steigerung an Komplexität zu den beiden vorhergehenden parallelen Auftragsblöcken erläutert. Problemanalyse für den Auftragsblock 101: Alle drei Aufträge sind nur dann erfüllbar, wenn der variable Auftrag K, ideal zwischen die beiden fixen Aufträge, V und A, gelegt wird. 4.4 "Schwierigkeitshierarchie" Die Aufgabenblöcke wurden entsprechend dem "subjektiven" Grad der Schwierigkeitseinschätzung in eine aufsteigende Reihenfolge gebracht. Eine empirische Erhebung zur Schwierigkeit steht zur Zeit noch aus. Die folgenden Auftragsblöcke sind nach ansteigender Auftragsanzahl gegliedert, da mit steigender Anzahl der Aufträge die Aufgabenbearbeitung zunehmend komplexer und damit voraussichtlich auch schwerer wird. Den höchsten Stellenwert bei der Konstruktion einer mutmaßlichen Schwierigkeitshierarchie hat die zeitliche Stabilität. Diese wird für jede Auftragsanzahl schrittweise aufgelöst, d.h. es liegen anfangs fixe, später variable Aufträge vor. Der Zwang zur Unvollständigkeit ist ein weiterer übergeordneter Faktor. Sobald die zeitliche Struktur weitgehend aufgelöst ist, wird der Zwang zur Unvollständigkeit eingeführt. In der fortlaufenden Schwierigkeitshierarchie wird dann versucht, auf jeder neuen Stufe zeitlicher Auflösung anschließend den Zwang zur Unvollständigkeit einzuführen. Über die gesamte Schwierigkeitshierarchie sollte je Auftragsanzahl die Häufigkeit der Überschneidungen von Aufträgen schrittweise erhöht werden. Bei dem Faktor der Anzahl von Überschneidungen handelt es sich jedoch um einen, der zeitlichen Stabilität und dem Zwang zur Unvollständigkeit, untergeordneten Faktor. Die Steigerung der Anzahl von Überschneidungen erfolgt deshalb oft nicht kontinuierlich, sondern ist von der Konstellation der anderen Faktoren abhängig. Alle weiteren oben angeführten Faktoren, die zeitliche Reihenfolge der Zeiträume, in denen variable Aufträge erledigt werden können und abhängige Aufträge, werden auf Basis der bereits genannten übergeordneten Faktoren eingeführt. Das zur Heuristik "Maximierung der Auftragserldigung" vorliegende Trainingsmaterial gliedert sich in Auftragsblöcke mit drei, vier oder fünf Aufträgen. Alle drei Typen werden nachfolgend kurz in ihren jeweiligen Schwierigkeitsabstufungen dargestellt. 4.4.1 Typ A3x: Auftragsblöcke zu drei Aufträgen: Auftragsblöcke zu drei Aufträgen liegen in folgenden Schwierigkeitsabstufungen (aufsteigende Schwierigkeit) vor: A Zu Beginn besteht eine relativ stabile zeitliche Ausgangssituation: es liegen zwei fixe Aufträge, ein variabler Auftrag und zwei Überschneidungen vor; Auftragsblöcke 101 und 102. B Die zeitliche Stabilität wird schrittweise aufgelöst: es liegen ein fixer Auftrag, zwei variable Aufträge und eine Überschneidung vor; Auftragsblöcke 103 und 104. C Bei gleicher zeitlicher Konstellation wie in B wird die Anzahl der Überschneidungen auf zwei erhöht; Auftragsblöcke 105 und 106. D Die Anzahl der Überschneidungen wird auf drei weiter erhöht; Auftragsblöcke 107 und 108. E Es erfolgt eine weitere zeitliche Destabilisierung: es liegen null fixe Aufträge, drei variable Aufträge und zwei Überschneidungen vor; Auftragsblöcke 109 und 110. F Zusätzlich wird die durch die Reihenfolge der Zeiträume vorgegebene implizite Bearbeitungsreihenfolge, in denen variable Aufträge erledigt werden können, umgekehrt; Auftragsblöcke 111 und 112. G Die Anzahl der Überschneidungen wird auf drei erhöht; Auftragsblöcke 113 und 114. H Der einfache Zwang zur Unvollständigkeit wird eingeführt, ein Auftrag ist im zeitlich forgegebenen Rahmen nicht lösbar. Die zeitliche Destabilisierung wird nochmals zurückgenommen, um die Einführung dieser neuen Schwierigkeit verständlich zu machen. Es liegen drei fixe Aufträge und zwei Überschneidungen vor; Auftragsblöcke 115 und 116. I Der einfache Zwang zur Unvollständigkeit wird beibehalten. Die zeitliche Stabilität wird wieder schrittweise aufgelöst: es liegen zwei fixe und ein variabler Auftrag vor. Die Anzahl der Überschneidungen wird auf drei erhöht; Auftragsblöcke 117 und 118. J Der einfache Zwang zur Unvollständigkeit und die Anzahl der Überschneidungen werden beibehalten, die zeitliche Stabilität weiter aufgelöst: es liegen ein fixer und zwei variable Aufträge vor; Auftragsblöcke 119 und 120. K Der einfache Zwang zur Unvollständigkeit und die Anzahl der Überschneidungen werden beibehalten. Die zeitliche Stabilität wird weitgehend aufgelöst: es liegen null fixe und drei variable Aufträge vor; Auftragsblöcke 121 und 122. 4.4.2 Typ A4x: Auftragsblöcke zu vier Aufträgen: Auftragsblöcke zu vier Aufträgen liegen in folgenden Schwierigkeitsabstufungen (steigende Schwierigkeit) vor: A Zu Beginn liegt eine hohe zeitliche Stabilität vor: vier fixe Aufträge und drei Überschneidungen. Der einfache Zwang zur Unvollständigkeit wird sofort eingeführt. Das Problem besteht darin, zwischen einem langen erledigbaren Auftrag oder drei kurzen erledigbaren Aufträgen sinnvoll abzuwägen; Auftragsblöcke 123 und 124. B Es liegt mit nur zwei Überschneidungen das gleiche Problem vor, allerdings ist die Abwägung nicht mehr so eindeutig und beträgt nunmehr zwei Aufträge zu drei Aufträgen, statt ein Auftrag zu drei Aufträgen; Auftragsblöcke 125 und 126. C Der Zwang zur Unvollständigkeit wird vorübergehend zurückgenommen, die zeitliche Stabilität statt dessen weiter aufgelöst. Es liegen drei fixe, ein variabler Auftrag und drei Überschneidungen vor; Auftagsblöcke 127 und 128. D Die zeitliche Stabilität wird schrittweise aufgelöst: es liegen zwei fixe, zwei variable Aufträge und drei Überschneidungen vor; Auftragsblöcke 129 und 130. E Zur bestehenden zeitlich vorgegebenen Struktur wird erneut der einfache Zwang zur Unvollständigkeit eingeführt, die Anzahl der Überschneidungen wird auf vier erhöht; Auftragsblöcke 131 und 132. F Der Zwang zur Unvollständigkeit wird wieder zurückgenommen, die zeitliche Struktur weiter aufgelöst: es liegen ein fixer, drei variable Aufträge und vier Überschneidungen vor; Auftragsblöcke 133 und 134. G Zur bestehenden zeitlich vorgegebenen Struktur wird wieder der einfache Zwang zur Unvollständigkeit eingeführt. Die Anzahl der Überschneidungen steigt auf sechs. Die Reihenfolge der Zeiträume, in denen die variablen Aufträge erledigt werden können, stimmt nicht mit der idealen Bearbeitungsreihenfolge der Aufträge überein; Auftragsblöcke 135 und 136. H Der Zwang zur Unvollständigkeit wird wieder zurückgenommen, die zeitliche Struktur statt dessen weiter aufgelöst: es liegen vier variable Aufträge vor. Die Anzahl der Überschneidungen beträgt weiterhin sechs; Auftragsblöcke 137 und 138. I Zur bestehenden zeitlich vorgegebenen Struktur wird nochmals der einfache Zwang zur Unvollständigkeit eingeführt. Die Anzahl der Überschneidungen bleibt gleich; Auftragsblöcke 139 und 140. 4.4.3 Auftragsblöcke zu fünf Aufträgen Auftragsblöcke zu fünf Aufträgen liegen in folgenden Schwierigkeitsabstufungen (steigende Schwierigkeit) vor: A Zu Beginn liegt eine hohe zeitliche Stabilität vor: der Auftragsblock besteht aus fünf fixen Aufträgen und vier Überschneidungen. Der einfache Zwang zur Unvollständigkeit wird eingeführt. Es muß abgewogen werden, ob ein langer oder vier kurze Aufträge bearbeitet werden; Auftragsblöcke 141 und 142. B Die zeitliche Stabilität und die Anzahl der Überschneidungen werden beibehalten. Der doppelte Zwang zur Unvollständigkeit wird eingeführt. Nun muß entschieden werden, ob drei oder zwei Aufträge bearbeitet werden. Die Schwierigkeit, die richtigen Aufträge auszuwählen, steigt an; Auftragsblöcke 143 und 144. C Die zeitliche Stabilität soll schrittweise aufgelöst werden: es liegen vier fixe, ein variabler Auftrag und vier Überschneidungen vor. Der Zwang zur Unvollständigkeit wird vorerst zurückgenommen; Auftragsblöcke 145 und 146. D Die zeitliche Stabilität wird beibehalten, der einfache Zwang zur Unvollständigkeit wieder eingeführt. Die Anzahl der Überschneidungen steigt auf fünf; Auftragsblöcke 147 und 148. E Es erfolgt eine weitere Auflösung der zeitlichen Stabilität: nun liegen drei fixe und zwei variable Aufträge vor. Der einfache Zwang zur Unvollständigkeit wird beibehalten, der Aufgabenbearbeiter muß entscheiden, ob er vier oder drei Aufträge erledigen möchte, und die entsprechende Wahl treffen. Die Anzahl der Überschneidungen steigt auf acht; Auftragsblöcke 149 und 150. F Die bestehende zeitliche Struktur wird beibehalten, die Anzahl der Überschneidungen sinkt auf sechs. Hinzu kommt der doppelte Zwang zur Unvollständigkeit. Es können wahlweise drei oder zwei Aufträge bearbeitet werden. Damit eine eindeutige Lösungsmöglichkeit gegeben ist, wird ein abhängiger Auftrag eingeführt. Es besteht eine inhaltliche Abhängigkeit von zwei Aufträgen, d.h. die Bearbeitung des zweiten (abhängigen) Auftrages setzt die Erledigung des anderen Auftrages voraus; Auftragsblöcke 151 und 152. G Die zeitliche Struktur wird weiter aufgelöst: es liegen zwei fixe und drei variable Aufträge vor, die Anzahl der Überschneidungen bleibt gleich. Die Reihenfolge der Zeiträume, in denen die variablen Aufträge zu bearbeiten sind, entspricht nicht der idealen Bearbeitungsreihenfolge der Aufträge. Der doppelte Zwang zur Unvollständigkeit wurde auf einen einfachen Zwang zur Unvollständigkeit reduziert; Auftragsblöcke 153 und 154. H Bei gleicher zeitlicher Ordnung wird der doppelte Zwang zur Unvollständigkeit erneut eingeführt. Die Anzahl der Überschneidungen steigt auf sieben; Auftragsblöcke 155 und 156. I Es erfolgt eine weitere zeitliche Destabilisierung: es liegen ein fixer, vier variable Aufträge und sechs Überschneidungen vor. Der doppelte Zwang zur Unvollständigkeit wird auf einen einfachen Zwang zur Unvollständigkeit reduziert; Auftragsblöcke 157 und 158. J Die zeitliche Struktur wird weitgehend aufgelöst, es liegen fünf variable Aufträge vor. Ferner wird der doppelte Zwang zur Unvollständigkeit wieder eingeführt, zugleich steigt die Anzahl der Überschneidungen auf zehn; Auftragsblöcke 159 und 160. 5Trainingseinheit "Minimierung der Wegzeiten" 5.1 Ziel des Trainings Die Heuristik "Minimierung der Wegzeiten" zielt im wesentlichen darauf ab, die räumliche Orientierung bzw. die richtige Einschätzung von Entfernungen mit Patienten zu trainieren. Ein weiteres Ziel dieser Trainingseinheit ist die Verbesserung des vorausschauenden Denkens (Antizipation). Entscheidend für die Auftragsbearbeitung ist in dieser Trainingsphase die angegebene Wegzeit zu den einzelnen Erledigungsorten und/oder deren räumliche Anordnung auf dem Bildschirm. Das einzige Auswahlkriterium soll in dieser Trainingseinheit die jeweils kürzeste Wegstrecke bzw. die kürzest mögliche Bearbeitungszeit eines Auftragsblocks (kurze Wegstrecken = kurze Bearbeitungszeit) sein. 5.2 Struktur der Auftragsblöcke Zur Isolierung der Heuristik "Wegzeitminimierung" wurden zwei verschiedene Grundstrukturen, einschrittige und zweischrittige Auftragsmuster, konstruiert. Erhöht man sukzessive die Anzahl der zu erledigenden Aufträge, so ist eine sinnvolle Bearbeitung der Heuristik "Wegzeitminimierung" aufgrund der räumlichen Anordnung der Orte auf dem Bildschirm nicht mehr möglich. Aus diesem Grund bestehen alle in Schritten konstruierten Auftragsblöcke aus maximal drei Aufträgen. Die Variation dieser Entscheidungsprobleme wurde u. a. mit Hilfe des sog. "Autovorteils" gelöst. Diese Option bietet die Möglichkeit, passend zur Heuristik, die zu bewältigenden Entfernungen in einem Drittel der sonst benötigten Wegzeit zurückzulegen. Ebenso optional ist die Angabe der Wegzeit in Minuten, die zur Erreichung der möglichen Erledigungsorte benötigt wird. Eine weitere Variation ergibt sich durch die Vorgabe der Anzahl der räumlichen Bezugspunkte, nach denen sich die Testperson richten kann. Die hier genannten Variationen beeinflussen auch die Schwierigkeit der unterschiedlichen Auftragsblöcke, in Kapitel 5.3 wird darauf noch näher eingegangen. Die Dauer der einzelnen Aufträge ist für die Heuristik irrelevant und wird deshalb in keinem der Auftragsblöcke angegeben. Ebenso verhält es sich mit konkreten Zeitpunkten, zu denen die Aufträge erledigt werden sollen; die Testperson hat zur Erledigung aller Aufträge eines Blocks den ganzen im Programm vorgesehenen Tag (10.00 - 18.00) Zeit. Um die verschiedenen Schwierigkeits- bzw. Komplexitätsgrade der hier ausgewählten Entscheidungsprobleme zu verdeutlichen, werden sie im folgenden (mit entsprechenden Beispielen im Text) graphisch dargestellt. Eine Übersicht über die in Schritten konstruierten Auftragsmuster zur Heuristik "Wegzeitminimierung" bietet Tabelle 5.1. Tab. 5.1: Darstellung der Auftragsmuster zur Heuristik "Wegzeitminimierung" Aufträge 2 3 Schritte 1. 1/2 1/3 2. - 1/2 3. - Die Tabelle 5.1 ist folgendermaßen zu lesen: Bestehen z. B. in einem Block drei Aufträge, so muß die Testperson im ersten Schritt den räumlich nächstgelegenen Auftrag aus den drei möglichen auswählen. Im zweiten Schritt soll wiederum der nächstgelegene Auftrag aus den beiden noch verbleibenden Aufträgen ausgewählt werden. Der dritte, bei optimaler Lösung des Auftragsblocks am weitesten entfernt liegende Auftrag soll aufgrund der bestehenden Heuristik von der Testperson nicht bearbeitet werden. Aus dieser Grundstruktur ergibt sich, daß unabhängig von der Auftragsanzahl immer ein Auftrag, nämlich der, der die meiste Wegzeit benötigt, außer acht gelassen werden soll. Um dieses Prinzip für die Testperson zu verdeutlichen, beginnen alle Aufträge, z.T. in leichten Abwandlungen, mit der Formulierung "Sie können heute ... (z. B.: im Café ein leckeres Stück Sahnetorte essen)." In Tabelle 5.2 sind ausgehend von den möglichen Startorten die für die Konstruktion der Aufträge entscheidenden Wegzeiten zu allen anderen Orten in Minuten angegeben. Tab. 5.2: Entfernungen der Erledigungsorte in Minuten vom jeweiligen Startort aus (1) P (2) C (3) K (4) S (5) V (6) B (7) W (8) Z (9) A C 10 P 10 S 14 K 14 C 19 A 12 V 21 W 24 B 12 S 26 V 19 A 25 W 24 W 21 K 36 S 24 V 45 K 25 V 29 S 28 P 30 V 26 S 26 S 50 Z 24 S 47 S 39 K 30 W 30 C 32 P 26 P 29 P 66 C 30 C 54 P 55 W 40 K 32 B 36 C 28 K 40 C 68 K 38 K 61 C 57 A 55 Z 54 W 38 A 39 Z 45 W 74 P 40 P 64 W 62 Z 64 A 57 V 40 Z 47 A 64 V 76 A 62 A 86 V 64 B 66 B 68 Z 61 B 50 B 76 Z 97 B 74 B 97 Z 86 Legende: P=Post, C=Café, K=Kulturzentrum, S=Supermarkt, V=Versicherung, B=Bank, W=Werkstatt, Z=Zuhause, A=Arzt. 5.3 Einflußfaktoren auf die Aufgabenschwierigkeit Die folgenden Faktoren beeinflussen die Schwierigkeit der Auftragsblöcke auf unterschiedliche Weise und beruhen auf theoretischen Überlegungen. Wie sich diese Einflüsse genau auswirken und ob zu den genannten Faktoren noch andere, hier nicht bedachte, hinzukommen, wird erst durch die praktische Anwendung dieser Trainingseinheit zu klären sein. Die hier gemachte Aufzählung ist deshalb auch nicht hierarchisch zu verstehen. 5.3.1 Anzahl der Aufträge in einem Auftragsblock Die Anzahl der Entscheidungen, die von der Testperson zur Lösung eines Auftragsblocks getroffen werden müssen ist abhängig von der Anzahl der Aufträge. Mit wachsender Auftragszahl werden die Blöcke zwar komplexer, dennoch steht die Testperson bei jedem Lösungsschritt vor einer Wahlentscheidung zwischen zwei Aufträgen und damit vor der Frage, welcher dieser Aufträge gemäß der Heuristik näher an ihrem jeweiligen Standort liegt. U.U. erweisen sich Auftragsblöcke mit drei Aufträgen als schwieriger als Blöcke mit nur zwei Aufträgen, da die Bearbeitungszeit dort umfangreicher ist und demnach auch mehr Konzentration erfordert. 5.3.2 Angabe der Wegzeit Die angegebene Wegzeit, die zur Erreichung der Einzelaufträge benötigt wird, erlaubt der Testperson eine präzise Beurteilung der Entfernung zum jeweiligen Erledigungsort. Werden die Wegzeiten nicht eingeblendet, ist die Testperson gezwungen, sich auf ihr räumliches Orientierungsvermögen bezüglich der Entfernungen der Erledigungsorte zu verlassen, welches sich, je nach Eindeutigkeit der Entfernungen, erheblich auf die Schwierigkeit der auszuführenden Aufträge auswirken kann. 5.3.3 Die Eindeutigkeit der Entfernung Die Entfernungen der Erledigungsorte auf dem Bildschirm sind aufgrund des vorhandenen Wegenetzes ohne Angabe der Wegzeit nicht immer eindeutig zu erkennen. Schwierig ist eine korrekte Entfernungsschätzung nach dem Muster "naher Ort vs. ferner Ort" insbesondere dann, wenn der Unterschied der Wegzeit zwischen zwei Orten weniger als 10 Minuten beträgt und / oder die Wegverbindungen "kurvenreich" sind. 5.3.4 Die Anzahl der Bezugspunkte Die vorhandenen räumlichen Bezugspunkte, die der Testperson bei der Wahlentscheidung für einen Auftrag zu Verfügung stehen, können ebenfalls die Schwierigkeit beeinflussen. Die Trainingseinheit stellt zwei Versionen zur Verfügung: Zum einen Auftragsblöcke mit einem Bezugspunkt, nämlich dem Startort (bzw. bei einer Auftragsanzahl von drei dem jeweiligen Standort), von dem aus eine Wahlentscheidung zwischen zwei Orten gemäß der Heuristik getroffen werden muß. Zum anderen gibt es Autragsblöcke mit zwei Bezugspunkten, dem Start- und dem Zielort, welche bei der Entscheidung für einen Erledigungsort beide mit einbezogen werden müssen. 5.3.5 Die Option "Autovorteil" Hat die Testperson in einem Auftragsblock die Möglichkeit, das Auto einmalig zu benutzen, so muß sie dessen Einsatz vorausschauend einplanen, d. h. sie muß vor der Ausführung der Aufträge abschätzen, welche die voraussichtlich längste zu bewältigende Wegstrecke sein wird, da dort der Autovorteil gemäß der Heuristik sinnvoll einzusetzen ist. 5.4 Einschrittige Auftragsmuster Da es sich bei den folgenden Abbildungen um schematische Darstellungen des jeweiligen Problems handelt, gibt die folgende Tabelle eine Auflistung der dort verwendeten Symbole. Tab. 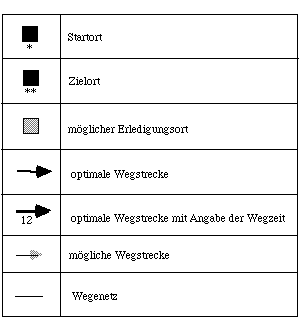5.3: Erläuterungen der in den Abbildungen 5.1 -5.6 verwendeten Symbole 5.4.1 Typ W1A: Auftragsblöcke mit zwei Aufträgen und Wegzeitangabe Der erste Auftragsblock besteht aus jeweils zwei Aufträgen, von denen einer nach dem Kriterium der kürzeren Wegstrecke, wie aus Abbildung 5.1 ersichtlich, auszuwählen und zu bearbeiten ist. Der räumliche Ausgangs- und Bezugspunkt ist, wie in allen weiteren Auftragsblöcken dieser Art, ein (variabler) Startort. Die Zeit, die zur Erreichung der beiden Erledigungsorte benötigt wird, ist in Minuten unter den Erledigungsorten auf dem Bildschirm angegeben. Damit kann eine präzisere Beurteilung der räumlichen Nähe erfolgen. Der Startort in Abbildung 5.1 der Ort V, von dem aus der nähergelegene Ort C (Wegzeit = 19 Minuten) anzusteuern ist. Der alternativ anzusteuernde Ort K ist vom Startort weiter entfernt (Wegzeit = 40 Minuten) und sollte deshalb von der Testperson nicht gewählt werden.Dieser Auftragsblock dient in erster Linie als Übung und zum Verständnis der zu beachtenden Heuristik. 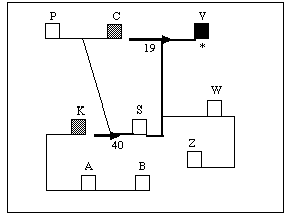Abb. 5.1: Veranschaulichung eines Problems vom Typ "W1A". Die Zahlen an den Pfeilen bedeuten Wegzeiten, die Buchstaben sind entsprechend der Legende von Tab. 5.2 zu interpretieren. Der * markiert den Startort, graue Blöcke stellen mögliche Erledigungsorte dar. 5.4.2 Typ W1B: Auftragsblöcke mit zwei Aufträgen ohne Wegzeitangabe In dieser Variante des ersten Typs wird die Wegzeit, die im vorangegangenen Auftragstyp der Testperson als Zusatzinformation zur Verfügung steht, nicht mehr dargeboten. Der räumliche Ausgangs- und Bezugspunkt ist in Abbildung 5.2 der Ort Z, von dem aus der nähergelegene Ort W anzusteuern ist. Der alternativ anzusteuernde Ort B ist, wenn man auf die Wegverbindung schaut, vom Startort deutlich weiter entfernt und sollte deshalb von der Testperson außer acht gelassen werden. 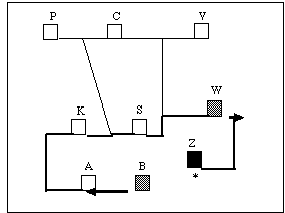Abb. 5.2: Veranschaulichung eines Problems vom Typ "W1B" zur "Wegzeitminimierung". Die Buchstaben sind entsprechend der Legende von Tab. 5.2 zu interpretieren. Der * markiert den Startort, graue Blöcke stellen mögliche Erledigungsorte dar. 5.4.3 Typ W1C: Auftragsblöcke mit zwei Aufträgen und Angabe des Zielortes Durch die Nennung von Start- und Zielort hat die Testperson hier statt einem (variablen) räumlichen/örtlichen Bezugspunkt, nämlich dem jeweiligen Standort, zwei feste Bezugspunkte, zu denen sie die Entfernung der in den Aufträgen genannten Erledigungsorte in Beziehung setzen muß. In diesem Auftragsblock soll die Testperson wiederum denjenigen von zwei möglichen Aufträgen erledigen, der am nächsten zwischen dem jeweils angegebenen Start- und Zielort liegt. Die Wegzeit ist, wie schon in Typ "W1A" als Zusatzinformation angegeben, jedoch gibt es hier die Möglichkeit, sie bei Bedarf auszublenden. Wie aus dem Beispiel in Abbildung 5.3 ersichtlich ist, trifft die Testperson die optimale Entscheidung, wenn sie den Auftrag am Ort S (Wegzeit K->S = 14, S->W = 24) und nicht den am weiter entfernten Ort V (Wegzeit K->V = 40, V->W = 21) ausführt. 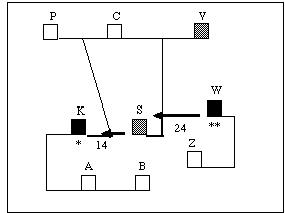Abb. 5.3: Veranschaulichung eines Problems vom Typ "W1C": Wegzeitminimierung mit einer Wahlentscheidung (hier: S oder V). Die Zahlen an den Pfeilen bedeuten Wegzeiten, die Buchstaben sind entsprechend der Legende von Tab. 5.2 zu interpretieren. Der * markiert den Startort, ** den Zielort, graue Blöcke stellen mögliche Erledigungsorte dar. 5.4.4 Typ W1D: Auftragsblöcke mit zwei Aufträgen und Angabe des Zielortes plus Autovorteil Im Auftragsblock des Typs W1D ist die einmalige Benutzung des "Autovorteils" vorgesehen. In diesem Fall muß die Testperson sich, wie oben beschrieben für einen von zwei möglichen Aufträgen entscheiden. Für die längere der beiden Wegstrecken in Abbildung 5.3 (K->S, S->W) sollte dann das Auto benutzt werden. Dies verlangt von der Testperson zusätzlich eine vorausschauende Abschätzung der Entfernungen zwischen den Orten K->S und S->W. Im Beispiel ist die längere (Auto)Strecke die zwischen den Orten S->W. 5.5 Zweischrittige Auftragsmuster 5.5.1 Typ W2A: Auftragsblöcke mit drei Aufträgen und Wegzeitangabe In diesem Auftragsblock wird die Testperson mit drei Aufträgen konfrontiert, von denen jeweils zwei nach dem Kriterium der kürzeren Wegstrecke auszuwählen sind. Bei optimaler Lösung dieses Problems befinden sich die Auftragsorte auf einer linearen Wegstrecke nach dem Muster A->B B->C, wobei ein möglicher Auftrag (D) aufgrund seiner Entfernung nicht bearbeitet werden soll. Ein Entscheidungsproblem ergibt sich für die Testperson dadurch, daß im ersten Schritt der nächstliegende Auftrag aus den drei möglichen und im zweiten Schritt wiederum der nächstliegende Auftrag aus den zwei verbleibenden Aufträgen ausgewählt werden soll. Der erste Aufgabentyp in dieser Klasse enthält als Zusatzinformation, wie Typ W1A, die explizite Angabe der Wegzeiten. 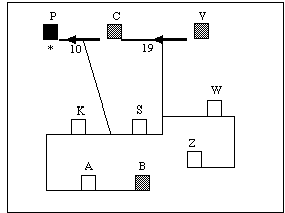Abb. 5.4: Veranschaulichung eines Problems vom Typ "W2A". Die Zahlen an den Pfeilen bedeuten Wegzeiten, die Buchstaben sind entsprechend der Legende von Tab. 5.2 zu interpretieren. Der * markiert den Startort, graue Blöcke stellen mögliche Erledigungsorte dar. In Abbildung 5.4 sind ausgehend vom Startort P Aufträge an den Orten B, C und V zu erledigen. Die optimale Bearbeitungsreihenfolge ergibt sich jeweils aus den angegebenen Wegzeiten, die von der Testperson vor der Wegstreckenentscheidung antizipiert und verglichen werden müssen. Im abgebildeten Beispiel wäre dies im ersten Schritt der Vergleich der Entfernungen der Orte C, V, B vom Startort P aus und im zweiten Schritt (bei korrekter Entscheidung in Schritt 1) der Vergleich der Entfernungen vom Ort C aus zu den Orten V und B. Da die auf dem Bildschirm angegebenen Entfernungen immer auf den jeweiligen Standort bezogen sind, ist für den Ort B, der bei jeder möglichen Wegstreckenentscheidung am weitesten entfernt liegt, keine Wegzeitangabe in Minuten dargestellt. 5.5.2 Typ W2B: Auftragsblöcke mit drei Aufträgen ohne Wegzeitangabe Dieser Typ unterscheidet sich vom voranstehenden durch die hier nicht eingeblendeten Wegzeiten. Auch dies soll wieder an einem Beispiel demonstriert werden. Abbildung 5.5 verdeutlicht dieses Problem. Ausgehend vom Startort Z sind Aufträge an den Orten A, V und W zu erledigen. Die optimale Bearbeitungsreihenfolge ergibt sich jeweils aus den sichtbaren Streckenlängen, die von der Testperson vor der Wegstreckenentscheidung verglichen werden müssen. Im abgebildeten Beispiel wäre dies im ersten Schritt der Vergleich der Entfernungen der Orte A, V, W vom Startort Z aus und im zweiten Schritt (bei korrekter Entscheidung in Schritt 1) der Vergleich der Entfernungen von Ort W aus zu den Orten V und A. 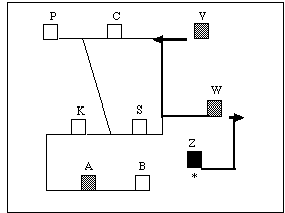Abb. 5.5: Veranschaulichung eines Problems vom Typ "W2B". Der * markiert den Startort, graue Blöcke stellen mögliche Erledigungsorte dar. 5.5.3 Typ W2C: Auftragsblöcke mit drei Aufträgen plus Autovorteil Wird zusätzlich zu dem oben beschriebenen Entscheidungsproblem die Möglichkeit gegeben, das Auto einmalig zu benutzen, so sollte dies, wiederum bei ausschließlicher Beachtung der Wegzeitminimierung, auf der längeren der beiden Teilstrecken geschehen. Auch hier wird zur Verdeutlichung der Entfernungen die Wegzeit zu den Erledigungsorten angegeben. Im Beispiel (Abb. 5.6) sollte das Auto für die erste zu bewältigende Strecke Z->W eingesetzt werden. 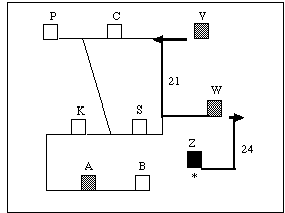Abb. 5.6: Veranschaulichung eines Problems vom Typ "W2C". Der * markiert den Startort, graue Blöcke stellen mögliche Erledigungsorte dar. 6 Trainingseinheit "Beachten der Priorität" 6.1 Ziel des Trainings Heuristiken sind Regeln, die bei Entscheidungen unter Unsicherheit als Entscheidungshilfen herangezogen werden (siehe 2.3). Wenn bei Entscheidungen unter Unsicherheit die Heuristik "Beachten der Priorität" als Entscheidungshilfe herangezogen wird, hat dies zur Folge, daß konkurrierende Entscheidungsmöglichkeiten gemäß ihrer jeweiligen Priorität in eine Rangreihe gebracht werden und nachfolgend diejenige Entscheidungsmöglichkeit ausgewählt wird, die in der Rangreihe den ersten Platz einnimmt. Diese Entscheidungsmöglichkeit weist eine höhere Priorität auf als die übrigen Entscheidungsmöglichkeiten der Menge. Zu der Heuristik "Beachten der Priorität" wurden Aufgabentypen konstruiert, bei denen in einer Menge möglicher Aufträge genau ein Auftrag enthalten ist, der eine höhere Priorität aufweist als alle übrigen Aufträge. Aus Gründen der Standardisierung und Vergleichbarkeit wurde die unterschiedliche Wichtigkeit der Aufträge induziert, die Priorität jedes einzelnen Auftrags ist eindeutig definiert (siehe 6.2). Die optimale Lösung einer Aufgabe besteht folglich darin, aus einer Menge möglicher Aufträge genau den Auftrag auszuwählen, der im Vergleich zu den übrigen Aufträgen dieser Menge die höchste Priorität aufweist. 6.2 Einflußfaktoren auf die Aufgabenschwierigkeit Die zu der Heuristik "Beachten der Priorität" konstruierten Aufgabentypen unterscheiden sich in ihrer Komplexität durch das Vorhandensein einer spezifischen Anzahl der nachfolgend genannten Komponenten. 6.2.1 Anzahl der Aufträge Ein Auftragsblock kann zwei bis neun Aufträge umfassen. Die Komplexität von Aufgabenblöcken eines Aufgabentypus¥ steigt mit der Anzahl an Aufträgen. 6.2.2 Anzahl der Schritte / Anzahl der Entscheidungen Ein zu bearbeitender Auftragsblock umfaßt einschrittige Auftragsmuster oder mehrschrittige Auftragsmuster. Die Komplexität eines Auftragsblocks steigt mit der Anzahl an Schritten, die in diesem Block enthalten sind. Die einschrittigen Auftragsmuster sind dadurch gekennzeichnet, daß in der Menge von 2, 3, 4, 5, 6, 7, 8 oder 9 Aufträgen genau ein Auftrag enthalten ist, der die höchste Priorität aufweist, alle anderen Aufträge weisen eine niedrigere Priorität auf bzw. sind mit keiner Prioritätsangabe versehen. Die optimale Lösung bei einschrittigen Auftragsmustern besteht darin, aus einer Menge möglicher Aufträge genau den Auftrag auszuwählen, der mit der höchsten Priorität versehen ist. Zur Konstruktion von einschrittigen Auftragsmustern kann auf die zeitliche Dimension noch verzichtet werden. In welchem zeitlichen Bezugssystem sich die Aufträge befinden, muß nicht notwendigerweise definiert werden. Wenn allerdings eine zeitliche Dimensionierung vorgenommen werden soll, ist es notwendig, alle Aufträge zeitlich parallel zu konstruieren, da andernfalls das Konzept der einschrittigen Auftragsmuster verlassen würde. Beispiel: einschrittiges Auftragsmuster ohne zeitliche Dimensionierung Sie müssen zur Bank WICHTIG Sie müssen zur Versicherung. WICHTIG Sie müssen zum CafÈ. Sie müssen zur Werkstatt. SEHR WICHTIG Sie müssen zum Kulturzentrum. optimale Lösung: Entscheidung für "Werkstatt" Beispiel: einschrittiges Auftragsmuster mit zeitlicher Dimensionierung Sie müssen um 15.00 Uhr zur Bank. WICHTIG Sie müssen um 15.00 Uhr zur Versicherung. WICHTIG Sie müssen um 15.00 Uhr zum CafÈ. Sie müssen um 15.00 Uhr zur Werkstatt. SEHR WICHTIG Sie müssen um 15.00 Uhr zum Kulturzentrum. optimale Lösung: Entscheidung für "Werkstatt" Durch die Beispiele soll deutlich werden, daß eine zeitliche Dimensionierung einschrittiger Auftragsmuster einzig dazu dient, die Komplexität der Auftragsbeschreibungen zu erhöhen. Sie hat für die Aufgabenlösung hingegen keinen Informationswert und ist aus diesem Grunde verzichtbar. Die Konstruktion mehrschrittiger Auftragsmuster ist nur unter der Bedingung möglich, daß ein zeitliches Bezugssystem für die Menge der Aufträge definiert wird. Während bei einschrittigen Auftragsmustern eine zeitliche Dimensionierung möglich, aber nicht zwingend ist, ist diese Dimensionierung bei mehrschrittigen Auftragsmustern zwingend, die Konstruktion eines mehrschrittigen Auftragsmusters bei Fehlen der zeitlichen Dimension nicht möglich. Mehrschrittige Auftragsmuster sind dadurch gekennzeichnet, daß sich die Menge aller Aufträge in Schritte einteilen läßt, die sich zeitlich nicht überschneiden, und in Untermengen, in denen ausschließlich Aufträge enthalten sind, die sich zeitlich überschneiden. Untermenge 1 Untermenge 2 Untermenge 3 Zeit Schritt 1 Schritt 2 Schritt 3 Abbildung 6.x : Veranschaulichung der Konzepte "Schritt" und "Untermenge" Legende: Untermenge Schritt Zeitstrahl Auftrag In den Untermengen 1, 2 und 3 sind jeweils zwei sich zeitlich überschneidende Aufträge enthalten. Die Schritte 1, 2 und 3 überschneiden sich hingegen zeitlich nicht. Beispiel: mehrschrittiges Auftragsmuster Sie müssen um 10.00 Uhr zur Bank. WICHTIG Sie müssen um 15.00 Uhr zum Kulturzentrum. Sie müssen um 10.00 Uhr zum CafÈ. SEHR WICHTIG Sie müssen um 12.00 Uhr zum Supermarkt. SEHR WICHTIG Sie müssen um 15.00 Uhr zur Post. WICHTIG Sie müssen um 12.00 Uhr zur Versicherung. 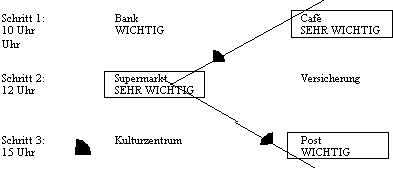optimale Lösung: Entscheidung für "CafÈ" Entscheidung für "Supermarkt" Entscheidung für "Post" Abbildung 6.x : Veranschaulichung der Entscheidungssequenz 6.2.3 Formulierung der Prioritätsangabe Die Aufgabentypen weisen zwei unterschiedliche Formen der Prioritätsangabe auf, die aber nie vermischt bei einem Aufgabentypus vorfindbar sind. Eine Form der Prioritätsangabe zeichnet sich dadurch aus, daß die einzelnen Aufträge eines Auftragsblocks explizit mit den Zusätzen "SEHR WICHTIG" oder "WICHTIG" versehen sind bzw. keinen Zusatz aufweisen. Die andere Form der Prioritätsnennung ist dadurch charakterisiert, daß sie in den Formulierungen der Auftragsinhalte enthalten ist. Die Prioritätsangabe erfolgt auch hier durch die Wörter "sehr wichtig" oder "wichtig", die objektives Entscheidungskriterium für die Wichtigkeit eines Auftrags sind. Subjektive Hypothesen über die Wichtigkeit eines Auftrags, die mit dem objektiven Kriterium - der Nennung der Wörter "sehr wichtig" oder "wichtig" - nicht übereinstimmen, führen nicht zur optimalen Lösung eines Auftragsblocks, sondern vielmehr zu Fehlern. Beispiele: "Dieser Termin ist wichtig.", "Sie haben einen sehr wichtigen Termin.", "Diese Verabredung ist Ihnen wichtig." usw. Die Komplexität einer Aufgabe ist höher, wenn die Prioritätsangaben in den Formulierungen des Auftragsinhalts enthalten sind. 6.2.4 Nennung des Auftragsinhalts Die Aufgabentypen unterscheiden sich dadurch, daß einige Typen keine Nennung der Auftragsinhalte enthalten, also keine Information darüber, was an einem Ort erledigt werden soll. Andere wiederum enthalten eine Nennung der Auftragsinhalte. Diese zwei Formen "Nennung des Auftragsinhalts" und "keine Nennung des Auftragsinhalts" kommen nicht vermischt bei einem Aufgabentypus vor. Die Komplexität von Aufgaben erhöht sich, wenn Nennungen des Auftragsinhalts im Auftragsblock enthalten sind. 6.3 Struktur der Auftragsblöcke Bei maximal neun Aufträgen eines Auftragsblocks sind die in Tabelle 6.1 dargestellten Auftragsmuster vorstellbar: Tabelle 6.1 zeigt in der ersten Zeile einschrittige Auftragsmuster, in den folgenden Zeilen sind mehrschrittige Auftragsmuster dargestellt. Aufträge Schritte 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 2 2-2 3-2 3-3 4-2 4-3 5-2 5-3 6-2 5-4 6-3 7-2 3 2-2-2 3-2-2 3-3-2 4-2-2 3-3-3 5-2-2 4-3-2 4 2-2-2-2 3-2-2-2 Beispiel: Bei acht Aufträgen und vier Schritten ergibt sich das Auftragsmuster 2-2-2-2. Dieses Auftragsmuster enthält vier Schritte, die sich zeitlich nicht überschneiden und vier Untermengen, die jeweils zwei sich zeitlich überschneidende Aufträge enthalten. 6.3.1 Einschrittige Auftragsblöcke Die hier vorfindbaren zwei Typen werden Typ P1A und Typ P1B genannt. Ihre Eigenschaften werden nachfolgend beschrieben. 6.3.1.1 Typ P1A Äußere Form: Auftragsblöcke vom Typ P1A umfassen zwei bis neun Aufträge. Auftragsblöcke vom Typ P1A sind immer einschrittig, d.h. es ist eine Entscheidung zur Problemlösung nötig. Die Prioritätsangabe erfolgt durch die Zusätze "SEHR WICHTIG" und "WICHTIG" bzw. keine Angabe zur Priorität. Bei Auftragsblöcken vom Typ P1A werden die Auftragsinhalte nicht benannt, die Aufträge sind standardisiert formuliert: "Sie müssen zu Ort X.". Einzige Variable ist "Ort X". Problemanalyse: Aus einer Menge von Aufträgen soll derjenige Auftrag ausgewählt werden, der die höchste Priorität aufweist. Beispiel: Sie müssen zum Arzt. WICHTIG Sie müssen zum Kulturzentrum. Sie müssen zur Versicherung. SEHR WICHTIG Konfigurationen: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 6.3.1.2 Typ P1B Äußere Form: Auftragsblöcke vom Typ P1B umfassen zwei bis neun Aufträge. Auftragsblöcke vom Typ P1B sind immer einschrittig, d.h. es ist eine Entscheidung zur Problemlösung nötig. Die Prioritätsnennung ist in den Formulierungen der Auftragsinhalte enthalten, objektives Entscheidungskriterium für die Wichtigkeit eines Auftrags ist das Vorhandensein der Wörter "sehr wichtig" und "wichtig". Bei Auftragsblöcken vom Typ P1B werden Auftragsinhalte benannt, Auftäge sind bei diesem Typ nicht standardisiert formuliert, enthalten allerdings - neben dem Auftragsinhalt - Angaben zum Auftragsort. Problemanalyse: Aus einer Menge von Aufträgen soll derjenige Auftrag ausgewählt werden, der die höchste Priorität aufweist. Im Unterschied zu Typ P1A muß allerdings zwischen mehreren Informationen diskriminiert werden, von denen einige für die Problemlösung wichtig, andere hingegen zu vernachlässigen sind. Beispiel: Sie haben schon seit einiger Zeit Halsschmerzen und befürchten, an einer Grippe zu erkranken. Um dies zu verhindern, ist es wichtig, Ihren Termin beim Arzt wahrzunehmen. Sie sind mit einem Bekannten im Kulturzentrum verabredet, wo Sie eine Fotoausstellung besuchen möchten. Sie möchten sich vom Kundenberater Ihrer Versicherung über die neuesten Versicherungsmöglichkeiten informieren lassen. Dieser Termin ist sehr wichtig. Konfigurationen: 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 6.3.2 Mehrschrittige Auftragsblöcke Die hier vorfindbaren drei Typen werden Typ PnC, Typ PnD und Typ PnE genannt, wobei n für die Anzahl der zu treffenden Entscheidungen (bzw. für die Anzahl der Schritte im Auftragsblock) steht. Ihre Eigenschaften werden nachfolgend beschrieben. 6.3.2.1 Typ PnC Äußere Form: Auftragsblöcke vom Typ PnC umfassen vier bis neun Aufträge. Auftragsblöcke vom Typ PnC sind immer mehrschrittig, d.h. sie umfassen zwei, drei oder vier Schritte. Es sind zwei, drei oder vier Entscheidungen zur Problemlösung nötig. Die Prioritätsangabe erfolgt durch die Zusätze "SEHR WICHTIG" und "WICHTIG" bzw. keine Angabe zur Priorität. Bei Auftragsblöcken vom Typ PnC werden die Auftragsinhalte nicht benannt, die Aufträge sind standardisiert formuliert: "Sie müssen um Y Uhr zu Ort X.". Variablen sind "Ort X" und "Zeit Y". Die Variable "Zeit Y" umfaßt ausschließlich feste Zeitpunkte. Problemanalyse: Durch die Einführung der zeitlichen Dimension muß in jeder Untermenge derjenige Auftrag identifiziert werden, der die höchste Priorität aufweist. Aus zwei, drei oder vier Untermengen soll jeweils derjenige Auftrag ausgewählt werden, der im Vergleich zu den übrigen Aufträgen der Untermenge die höchste Priorität aufweist. Beispiel: Sie müssen um 15.00 Uhr zum Arzt. WICHTIG Sie müssen um 12.15 Uhr zum Kulturzentrum. Sie müssen um 15.00 Uhr zur Versicherung. SEHR WICHTIG Sie müssen um 12.15 Uhr zum Supermarkt. WICHTIG Konfigurationen: 33, 34, 35, 36, 37, 38 6.3.2.2 Typ PnD Äußere Form: Auftragsblöcke vom Typ PnD umfassen vier bis neun Aufträge. Auftragsblöcke vom Typ PnD sind immer mehrschrittig, d.h. sie umfassen zwei, drei oder vier Schritte. Es sind zwei, drei oder vier Entscheidungen zur Problemlösung nötig. Die Prioritätsnennung ist in den Formulierungen der Auftragsinhalte enthalten, objektives Entscheidungskriterium für die Wichtigkeit eines Auftrags ist das Vorhandensein der Wörter "sehr wichtig" und "wichtig". Bei Auftragsblöcken vom Typ PnD werden Auftragsinhalte benannt, Aufträge sind nicht standardisiert formuliert, enthalten allerdings immer - neben dem Auftragsinhalt - Angaben zum Auftragsort und zum festen Zeitpunkt des Auftrags. Problemanalyse: Durch die Einführung der zeitlichen Dimension muß in jeder Untermenge derjenige Auftrag identifiziert werden, der die höchste Priorität aufweist. Aus zwei, drei oder vier Untermengen soll jeweils derjenige Auftrag ausgewählt werden, der im Vergleich zu den übrigen Aufträgen der Untermenge die höchste Priorität aufweist. Im Unterschied zu Typ PnC muß allerdings zwischen mehreren Informationen diskriminiert werden, von denen einige für die Problemlösung wichtig, andere hingegen zu vernachlässigen sind. Beispiel: Sie haben schon seit einiger Zeit Halsschmerzen und befürchten, an einer Grippe zu erkranken. Um dies zu verhindern, ist es wichtig, Ihren Termin um 15.00 Uhr beim Arzt wahrzunehmen. Sie sind um 12.15 Uhr mit einem Bekannten im Kulturzentrum verabredet, wo Sie eine Fotoausstellung besuchen möchten. Sie möchten sich vom Kundenberater Ihrer Versicherung über die neuesten Versicherungsmöglichkeiten informieren lassen. Dieser Termin um 15.00 Uhr ist sehr wichtig. Es ist wichtig für Sie, um 12.15 Uhr im Supermarkt zu sein, um dort noch von den verlockenden Sonderangeboten profitieren zu können, bevor sie ausverkauft sind. Konfigurationen: 39, 40, 41, 42, 43, 44 6.3.2.3 Typ PnE Äußere Form: Auftragsblöcke vom Typ PnE umfassen vier bis neun Aufträge. Auftragsblöcke vom Typ PnE sind immer mehrschrittig, d.h. sie umfassen zwei, drei oder vier Schritte. Es sind zwei, drei oder vier Entscheidungen zur Problemlösung nötig. Die Prioritätsangabe erfolgt durch die Zusätze "SEHR WICHTIG" und "WICHTIG" bzw. keine Angabe zur Priorität. Bei Auftragsblöcken vom Typ PnE werden die Auftragsinhalte nicht benannt, die Aufträge sind standardisiert formuliert: "Sie müssen um Y Uhr zu Ort X." bzw. "Sie müssen von Y Uhr bis Y Uhr zu Ort X.". Variablen sind "Ort X" und "Zeit Y". Die Variable "Zeit Y" umfaßt Aufträge mit festen Zeitpunkten ("um Y Uhr") und Aufträge mit festen Anfangs- und Endzeitpunkten ("von Y Uhr bis Y Uhr"). Problemanalyse: Durch die Einführung der zeitlichen Dimension muß in jeder Untermenge derjenige Auftrag identifiziert werden, der die höchste Priorität aufweist. Aus zwei, drei oder vier Untermengen soll jeweils derjenige Auftrag ausgewählt werden, der im Vergleich zu den übrigen Aufträgen der Untermenge die höchste Priorität aufweist. Beispiel: Sie müssen um 15.00 Uhr zum Arzt. WICHTIG Sie müssen von 11.15 Uhr bis 12.30 Uhr Uhr zum Kulturzentrum. Sie müssen von 14.30 Uhr bis 15.15 Uhr zur Versicherung. SEHR WICHTIG Sie müssen um 12.15 Uhr zum Supermarkt. WICHTIG Konfigurationen: 45, 46, 47, 48, 49, 50 Tabelle 6.2: Auftragstypen im Vergleich Anzahl der Aufträge Anzahl der Schritte Prioritätsangabe Nennung des Auftragsinhalts zeitliche Dimensionierung Typ P1A 2, 3, 4, 5, 6, 7, 8, 9 1 explizit nein nein Typ P1B 2, 3, 4, 5, 6, 7, 8, 9 1 implizit ja nein Typ PnC 4, 5, 6, 7, 8, 9 2, 3, 4 explizit nein feste Zeitpunkte Typ PnD 4, 5, 6, 7, 8, 9 2, 3, 4 implizit ja feste Zeitpunkte Typ PnE 4, 5, 6, 7, 8, 9 2, 3, 4 explizit nein feste Zeitpunkte und Zeiträume 7 Ausblick Die hier vorgestellte Konzeption eines systematischen Programms zur Diagnostik und zum Training von Planungskompetenz bedarf natürlich einer empirischen Überprüfung. Diese Überprüfung kann nur gelingen, wenn Daten aus Praxiseinrichtungen in genügend großer Zahl erhoben werden können. Sollten sich Praxiseinrichtungen finden, die zur Erprobung unseres Programms bereit sind, wäre unsere Arbeit auf fruchtbarenm Boden gefallen. Wir hoffen, daß in der möglichst engen Kooperation zwischen Programmentwicklung und praktischer Erprobung weitere Verbesserungen an dieser Konzeption möglich werden. Literatur Funke, J. & Krüger, T. (1995). Plan-a-Day: Konzeption eines modifizierbaren Instruments zur Führungskräfte-Auswahl sowie erste empirische Befunde. In J. Funke & A. Fritz (Eds.), Neue Konzepte und Instrumente zur Planungsdiagnostik (pp. 97-120). Bonn: Deutscher Psychologen Verlag. Kohler, J.A., Krüger, T. & Funke, J. (1996). Diagnostik und Therapie von Planungsstörungen mit Hilfe von Plan-A-Day. Manuskript zum Poster, präsentiert auf der 11. Jahrestagung der GNP in Bad Wildungen vom 3.-6.10. 1996. Kohler, J.A., Poser, U. & Schönle, W. (1995). Die Verwendung von Plan-a-Day für die neuropsychologische Diagnostik und Therapie. In J. Funke & A. Fritz (Eds.), Neue Konzepte und Instrumente zur Planungsdiagnostik (pp. 167-181). Bonn: Deutscher Psychologen Verlag. Danksagung Die Arbeiten an diesem Programm sind stark motiviert worden durch Anregungen, die praktisch tätige Neuropsychologen an uns herangetragen haben. Neben Dr. Joachim Kohler (Fachklinik Bad Aibling) ist hier auch Dipl.-Psych. Dr. Hans-Peter Steingass (Haus Remscheid) zu nennen. Durch differenziertes Feedback haben beide Personen dazu beigetragen, unsere Konzeption zu verbessern. Dafür sagen wir herzlichen Dank!	Startseite BMFT project Complex problem solving Complex problem solving research - Homepage DFG-Projekt SMT DYNAMIS DFG-Projekt Kompetenzdiagnostik Blickbewegung DRK Hotline-Schulung Gummibären-Forschung Internet Research KOGNI Program Description Forschungsthema: Neuropsychologie Complex Problem Solving: Research Principles Plan-a-Day   Plan-a-Day ACT-R model   Therapie von Planungsstörungen mit Hilfe von Plan-A-Day   Plan-a-Day Interface   Therapie von Planungsstörungen mit Hilfe von Plan-A-Day - Manual Research on Complex Problem Solving (Komplexes Problemlösen)
	Top Zuletzt bearbeitet am 30.08.2007 von JF.