

Forschung > DYNAMIS > DYNAMIS Approach
DYNAMIS Approach
The DYNAMIS approach to Complex Problem Solving (CPS) is a way of systematic construction and precise description of small-scale complex systems. For this purpose, it uses the formalism of Linear Structural Equations (LSE).
In everyday life, a number of activities require the regulation and control of processes which consist of quantitative variables (e.g., driving a car, controlling a CAD-machine). Not only technical but also economic and ecological situations require that we first have to understand the system before goal-oriented action is possible. In many sciences, systems with quantitative variables are represented successfully by means of the general linear model.
How can such a linear model be used as a tool for analyzing decision making and problem solving? The subject is instructed that she or he has to deal with a system that consists of some exogenous and endogenous variables. The exogenous ones can be directly manipulated by the subject and, thus, can influence the endogenous variables which can not be manipulated directly. The general task is (a) to find out how the exo- and endogenous variables are related to each other, and (b) to control the variables in the system so that they reach certain goal values. Normally, these two subtasks of system identification and system control are separated experimentally as two steps of the whole task (see Funke, 1993).
The basic structure of a simple linear system, for example, consisting of four variables is shown in Figure 1 (adopted from Vollmeyer & Funke, 1999). Instead of labeling the variables semantically, abstract letters are used. A system which contains semantics from biology can be found in Vollmeyer, Burns, and Holyoak (1996).
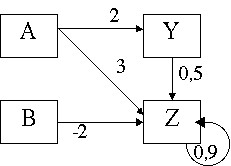
In the example system from Figure 1, the variables A and B represent the exogenous variables which have an effect on the endogenous variables Y and Z. The numbers on the arrows represent the weight with which the respective exogenous variables affect the endogenous ones. The system is described formally by two equations (one for each endogenous variable):
Yt+1 = 2 * At (1)
Zt+1 = 3 * At - 2 * Bt + 0,5 * Yt + 0,9 * Zt (2)
In these equations, the indices t and t+1 represent the actual state of the system which itself goes on in discrete steps (=periods) on the time axis. From equation (1) it turns out that the value of Y at period t+1 can be calculated from the value of A at period t, times two. Similar, in equation (2) the value of Z at t+1 can be calculated from the exogenous variables A and B at period t (with weight 3 and -2), from the value of Y at that time (weight 0,5), and from its own value at period t times 0.9. Normally, such a system is presented on a screen where all the variables are shown together with the system's history (for a certain period of time). What is not shown to the subjects is the structure of the system because it has to be discovered by them during the exploration phase.
In some systems, the endogenous variables have effects on other endogenous ones (in Figure 1, the effect from Y to Z), an effect which one might label as "indirect effect" which shows up only in case of manipulating the exogenous variable A. This variable A has itself two effects, one being larger ("main effect" on Z), one being smaller ("side effect" on Y). Also, endogenous variables can influence themselves (in the example shown with variable Z), thus representing an effect one might call "eigendynamic" because of the constant increase or decrease of this variable independent of other influences. As the reader might imagine, there are many possibilities to construct linear systems with a full range of effects of the kind described above and, thus, making identification and control of such systems to a hard problem.
References
- Blech, C., & Funke, J. (2005). Dynamis review: An overview about applications of the Dynamis approach in cognitive psychology. Heidelberg University: Unpublished manuscript. [Download as PDF]
- Funke, J. (1993). Microworlds based on linear equation systems: A new approach to complex problem solving and experimental results. In G. Strube & K.-F. Wender (Eds.), The cognitive psychology of knowledge (pp. 313-330). Amsterdam: Elsevier Science Publishers. [Download as PDF]
- Vollmeyer, R., & Funke, J. (1999). Personen- und Aufgabenmerkmale beim komplexen Problemlösen. Psychologische Rundschau, 50, 213-219.
- Vollmeyer, R., Burns, B. D., & Holyoak, K. J. (1996). The impact of goal specificity on strategy use and the acquisition of problem structure. Cognitive Science, 20, 75-100.
Get more info: DYNAMIS Research Groups
Zuletzt bearbeitet am 13.09.2005 von JF. |